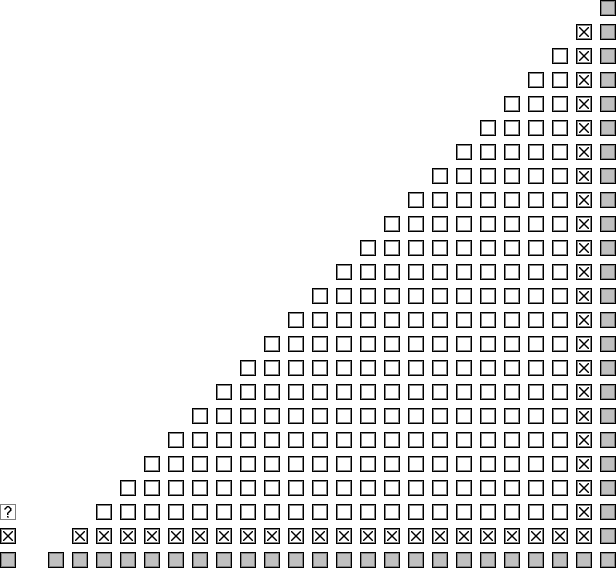
In the same way, let's consider the guest 23. It can't be W, because she shook at the most the hands of 24, and of 2 to 22. Actually, she can't have shaken the hand of M because he is her husband, nor 0's one because he shook none, nor 1's one, because he shook only 24's one), nor her own, so at the most 22. So, 23 must be part of the 11 other couples ((M, W) and (24, 0) being excluded). Using the same reasoning as before, we establish that the hands shaken by 23 are the ones from 2 to 22, plus necessarily M's one, what rises to 2 the number of hands he has shaken, as the following schema shows.
Let's note that the spouse of 23 is inevitably 1. In fact, in can neither be from 2 to 22 because he shook their hands, nor 24 or 0 because they are a couple already, nor, of course, M because we said 23 is not F. So, we have a second couple (23, 1).

All we have to do now is to reiterate the method from 22 to 13. We obtain 10 new couples: (22, 2), (21, 3), (20, 4), (19, 5), (18, 6), (17, 7), (16, 8), (15, 9), (14, 10) et (13, 11). As for the two first stages, we note that M shakes one hand for each couple, that is 12. While processing the couple (13, 11), we obtain the following schema:
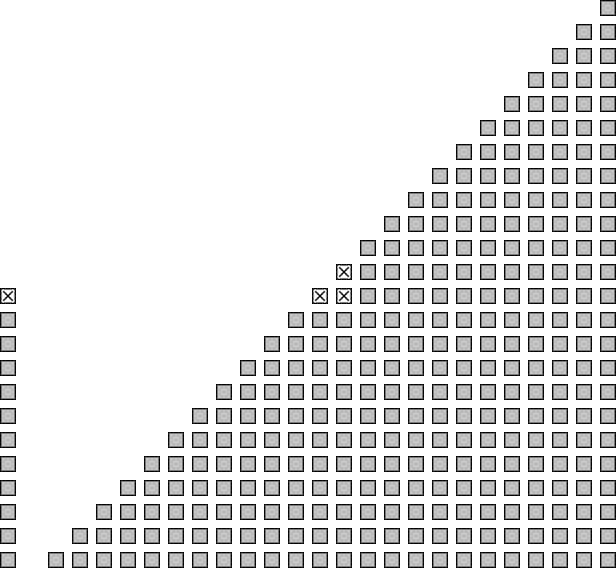
The only guest that is still alone is 12, who must be the wife W of M. So we obtain the solution of the enigma:
The man had shaken 12 hands, and so did his wife.